HW10. Diffusion Model and Epipolar Geometry
Topics: Diffusion model, Multi-head attention, Fundamental matrix, Homogeneous coordinates
Problem 1: Diffusion model
In this problem, you will be implementing some parts of the denoising diffusion probabilistic model. Specifically, you will need to implement the attention layer in the model architecture and the classifier-free guidance for sampling. Finally you’ll be able to train a model that can generate images with Cifar-10 dataset. Have fun!
# Imports
from contextlib import contextmanager
from copy import deepcopy
from glob import glob
import math, os, random
from matplotlib.pyplot import imread # alternative to scipy.misc.imread
import matplotlib.patches as patches
import os.path
from os.path import *
from IPython import display
from matplotlib import pyplot as plt
import torch
from torch import optim, nn, Tensor
from torch.nn import functional as F
from torch.utils import data
from torchvision import datasets, transforms, utils
from torchvision.transforms import functional as TF
from tqdm.notebook import tqdm, trange
import numpy as np
import math
# Utilities
@contextmanager
def train_mode(model, mode=True):
"""A context manager that places a model into training mode and restores
the previous mode on exit."""
modes = [module.training for module in model.modules()]
try:
yield model.train(mode)
finally:
for i, module in enumerate(model.modules()):
module.training = modes[i]
def eval_mode(model):
"""A context manager that places a model into evaluation mode and restores
the previous mode on exit."""
return train_mode(model, False)
@torch.no_grad()
def ema_update(model, averaged_model, decay):
"""Incorporates updated model parameters into an exponential moving averaged
version of a model. It should be called after each optimizer step."""
model_params = dict(model.named_parameters())
averaged_params = dict(averaged_model.named_parameters())
assert model_params.keys() == averaged_params.keys()
for name, param in model_params.items():
averaged_params[name].mul_(decay).add_(param, alpha=1 - decay)
model_buffers = dict(model.named_buffers())
averaged_buffers = dict(averaged_model.named_buffers())
assert model_buffers.keys() == averaged_buffers.keys()
for name, buf in model_buffers.items():
averaged_buffers[name].copy_(buf)
1.(a) implement multi-head attention
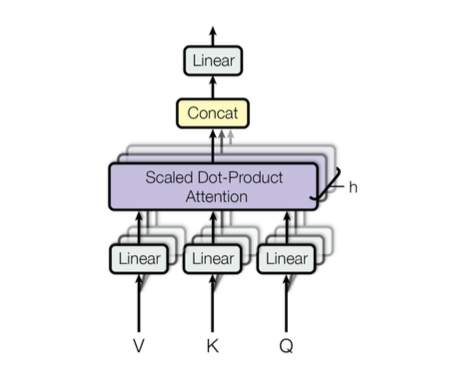
You will be implementing the multihead attention. Specifically, you’ll implement two classes: SelfAttention and MultiHeadAttention. Single head self attention takes a sequence x with shape (N, K, M) as input and outputs three matrices Q, K, V. Each of the matrices is a linear transformation of x. The attention is then calculated with:
\[\operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) V,\]where $d_k$ is the last dimension of K.
Multi-head attention is the concatenation of several single head attentions.
\[\begin{aligned} \operatorname{MultiHead}(Q, K, V) &=\operatorname{Concat}\left(\operatorname{head}_1, \ldots, \operatorname{head}_{\mathrm{h}}\right) W^O \\ \text { where }\operatorname{head}_\mathrm{i} &=\operatorname{Attention}\left(Q W_i^Q, K W_i^K, V W_i^V\right) \end{aligned}\]Each projection layer changes the size of input to $\frac{d_{out}}{\text{num_heads}}$.
A final linear layer with weight $W^O$ maps back to the input dimension.
class SelfAttention(nn.Module):
def __init__(self, dim_in: int, dim_q: int, dim_v: int):
super().__init__()
"""
This class is used for calculating single head attention.
You will first initialize the layers, then implement
(QK^T / sqrt(d_k))V in function scaled_dot_product.
Finally you'll need to put them all together into the forward funciton.
args:
dim_in: an int value for input sequence embedding dimension
dim_q: an int value for output dimension of query and ley vector
dim_v: an int value for output dimension for value vectors
"""
self.q = None # initialize for query
self.k = None # initialize for key
self.v = None # initialize for value
##########################################################################
# TODO: This function initializes three linear layers to get Q, K, V. #
# Please use the same names for query, key and value transformations #
# as given above. self.q, self.k, and self.v respectively. #
##########################################################################
# Replace "pass" statement with your code
self.q = nn.Linear(dim_in, dim_q)
self.k = nn.Linear(dim_in, dim_q)
self.v = nn.Linear(dim_in, dim_v)
##########################################################################
# END OF YOUR CODE #
##########################################################################
def scaled_dot_product(self,
query: Tensor, key: Tensor, value: Tensor
) -> Tensor:
"""
The function performs a fundamental block for attention mechanism, the scaled
dot product.
args:
query: a Tensor of shape (N,K, M) where N is the batch size, K is the
sequence length and M is the sequence embeding dimension
key: a Tensor of shape (N, K, M) where N is the batch size, K is the
sequence length and M is the sequence embeding dimension
value: a Tensor of shape (N, K, M) where N is the batch size, K is the
sequence length and M is the sequence embeding dimension
return:
y: a tensor of shape (N, K, M) that contains the weighted sum of values
"""
y = None
###############################################################################
# TODO: This function calculates (QK^T / sqrt(d_k))V on a batch scale. #
# Implement this function using no loops. #
###############################################################################
# Replace "pass" statement with your code
y = torch.matmul(query, key.mT) / math.sqrt(key.shape[2])
y = nn.Softmax(dim = -1)(y)
y = torch.matmul(y, value)
##############################################################################
# END OF YOUR CODE #
##############################################################################
return y
def forward(
self, query: Tensor, key: Tensor, value: Tensor
) -> Tensor:
"""
An implementation of the forward pass of the self-attention layer.
args:
query: Tensor of shape (N, K, M)
key: Tensor of shape (N, K, M)
value: Tensor of shape (N, K, M)
return:
y: Tensor of shape (N, K, dim_v)
"""
y = None
##########################################################################
# TODO: Implement the forward pass of attention layer with functions #
# defined above. #
##########################################################################
# Replace "pass" statement with your code
Q = self.q(query)
K = self.k(key)
V = self.v(value)
y = self.scaled_dot_product(Q, K, V)
##########################################################################
# END OF YOUR CODE #
##########################################################################
return y
class MultiHeadAttention(nn.Module):
def __init__(self, num_heads: int, dim_in: int, dim_out: int, dropout_rate:float = 0.1):
super().__init__()
"""
A naive implementation of the MultiheadAttention layer. You will apply
the self attention defined above and concat them together to calculate
multi-head attention.
args:
num_heads: int value specifying the number of heads
dim_in: int value specifying the input dimension of the query, key
and value. This will be the input dimension to each of the
SingleHeadAttention blocks
dim_out: int value specifying the output dimension of the complete
MultiHeadAttention block
"""
##########################################################################
# TODO: Initialize two things here: #
# 1.) Use nn.ModuleList to initialze a list of SingleHeadAttention layer #
# modules.The length of this list should be equal to num_heads with each #
# SingleHeadAttention layer having input dimension as dim_in, and the #
# last dimension of concated heads should be d_out #
# 2.) Use nn.Linear to map the output of nn.Modulelist block back to #
# dim_in. #
##########################################################################
# Replace "pass" statement with your code
self.attention_list = nn.ModuleList()
for i in np.arange(num_heads):
single_attention = SelfAttention(dim_in, int(dim_out / num_heads), int(dim_out/ num_heads))
self.attention_list.append(single_attention)
self.final_layer = nn.Linear(dim_out, dim_in)
##########################################################################
# END OF YOUR CODE #
##########################################################################
self.dropout = nn.Dropout(dropout_rate)
self.norm = nn.LayerNorm(dim_out)
def forward(
self, x: Tensor
) -> Tensor:
"""
An implementation of the forward pass of the MultiHeadAttention layer.
args:
query: Tensor of shape (N, K, M) where N is the number of sequences in
the batch, K is the sequence length and M is the input embedding
dimension. M should be equal to dim_in in the init function
key: Tensor of shape (N, K, M) where N is the number of sequences in
the batch, K is the sequence length and M is the input embedding
dimension. M should be equal to dim_in in the init function
value: Tensor of shape (N, K, M) where N is the number of sequences in
the batch, K is the sequence length and M is the input embedding
dimension. M should be equal to dim_in in the init function
returns:
y: Tensor of shape (N, K, M)
"""
y = None
n, c, h, w = x.shape
x = x.reshape(n, c, h*w).transpose(-2, -1)
query, key, value = x, x, x
##########################################################################
# TODO: Implement the forward pass of multi-head attention layer with #
# functions defined above. #
##########################################################################
# Replace "pass" statement with your code
results = []
for i in range(0, len(self.attention_list)):
res = self.attention_list[i](query, key, value)
results.append(res)
y = torch.cat(results, dim = 2)
y = self.final_layer(y)
##########################################################################
# END OF YOUR CODE #
##########################################################################
# Residual connection, normalization and dropout
return self.dropout(self.norm(x) + y).transpose(-2, -1).reshape(n, c, h, w)
# Define the model (a residual U-Net)
class ResidualBlock(nn.Module):
def __init__(self, main, skip=None):
super().__init__()
self.main = nn.Sequential(*main)
self.skip = skip if skip else nn.Identity()
def forward(self, input):
return self.main(input) + self.skip(input)
class ResConvBlock(ResidualBlock):
def __init__(self, c_in, c_mid, c_out, is_last=False):
skip = None if c_in == c_out else nn.Conv2d(c_in, c_out, 1, bias=False)
super().__init__([
nn.Conv2d(c_in, c_mid, 3, padding=1),
nn.Dropout2d(0.1, inplace=True),
nn.ReLU(inplace=True),
nn.Conv2d(c_mid, c_out, 3, padding=1),
nn.Dropout2d(0.1, inplace=True) if not is_last else nn.Identity(),
nn.ReLU(inplace=True) if not is_last else nn.Identity(),
], skip)
class SkipBlock(nn.Module):
def __init__(self, main, skip=None):
super().__init__()
self.main = nn.Sequential(*main)
self.skip = skip if skip else nn.Identity()
def forward(self, input):
return torch.cat([self.main(input), self.skip(input)], dim=1)
class FourierFeatures(nn.Module):
def __init__(self, in_features, out_features, std=1.):
super().__init__()
assert out_features % 2 == 0
self.weight = nn.Parameter(torch.randn([out_features // 2, in_features]) * std)
def forward(self, input):
f = 2 * math.pi * input @ self.weight.T
return torch.cat([f.cos(), f.sin()], dim=-1)
def expand_to_planes(input, shape):
return input[..., None, None].repeat([1, 1, shape[2], shape[3]])
class Diffusion(nn.Module):
def __init__(self):
super().__init__()
c = 64 # The base channel count
self.timestep_embed = FourierFeatures(1, 16)
self.class_embed = nn.Embedding(11, 4)
self.net = nn.Sequential( # 32x32
ResConvBlock(3 + 16 + 4, c, c),
ResConvBlock(c, c, c),
SkipBlock([
nn.AvgPool2d(2), # 32x32 -> 16x16
ResConvBlock(c, c * 2, c * 2),
ResConvBlock(c * 2, c * 2, c * 2),
SkipBlock([
nn.AvgPool2d(2), # 16x16 -> 8x8
ResConvBlock(c * 2, c * 4, c * 4),
MultiHeadAttention(c * 4 // 64, c * 4, c * 4),
ResConvBlock(c * 4, c * 4, c * 4),
MultiHeadAttention(c * 4 // 64, c * 4, c * 4),
SkipBlock([
nn.AvgPool2d(2), # 8x8 -> 4x4
ResConvBlock(c * 4, c * 8, c * 8),
MultiHeadAttention(c * 8 // 64, c * 8, c * 8),
ResConvBlock(c * 8, c * 8, c * 8),
MultiHeadAttention(c * 8 // 64, c * 8, c * 8),
ResConvBlock(c * 8, c * 8, c * 8),
MultiHeadAttention(c * 8 // 64, c * 8, c * 8),
ResConvBlock(c * 8, c * 8, c * 4),
MultiHeadAttention(c * 4 // 64, c * 4, c * 4),
nn.Upsample(scale_factor=2, mode='bilinear', align_corners=False),
]), # 4x4 -> 8x8
ResConvBlock(c * 8, c * 4, c * 4),
MultiHeadAttention(c * 4 // 64, c * 4, c * 4),
ResConvBlock(c * 4, c * 4, c * 2),
MultiHeadAttention(c * 2 // 64, c * 2, c * 2),
nn.Upsample(scale_factor=2, mode='bilinear', align_corners=False),
]), # 8x8 -> 16x16
ResConvBlock(c * 4, c * 2, c * 2),
ResConvBlock(c * 2, c * 2, c),
nn.Upsample(scale_factor=2, mode='bilinear', align_corners=False),
]), # 16x16 -> 32x32
ResConvBlock(c * 2, c, c),
ResConvBlock(c, c, 3, is_last=True),
)
def forward(self, input, t, cond):
timestep_embed = expand_to_planes(self.timestep_embed(t[:, None]), input.shape)
class_embed = expand_to_planes(self.class_embed(cond + 1), input.shape)
return self.net(torch.cat([input, class_embed, timestep_embed], dim=1))
1.(b) implement sampling process of diffusion model
Implement classifier-free guidance in the sample function. Classifier- free guidance allows the diffusion model to generate class-conditioned samples without training an extra classifier. For each time step, the model generates both class-conditioned and and unconditioned velocity and compute with the following function to obtain the classifier-guided velocity.
\[\overset{\sim}\epsilon_{t} = w\epsilon_{\theta}(z_{t}, c) - (w - 1)\epsilon_{\theta}(z_t)\]In practice, you can first make a copy of z and t, and use -1 to indicate the class of unconditioned sample. Then stack the three things separately on the batch dimension to compute two velocity in parallel.
# Define the noise schedule and sampling loop
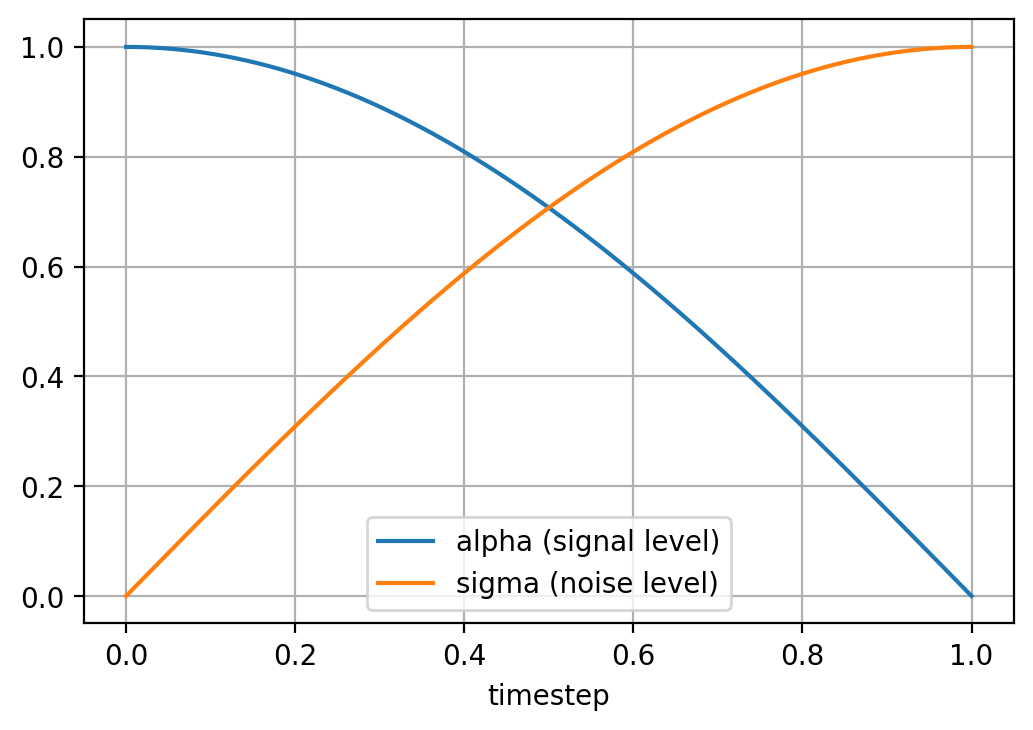
def get_alphas_sigmas(t):
"""Returns the scaling factors for the clean image (alpha) and for the
noise (sigma), given a timestep."""
return torch.cos(t * math.pi / 2), torch.sin(t * math.pi / 2)
@torch.no_grad()
def sample(model, x, steps, eta, classes, guidance_scale=1.):
"""Draws samples from a model given starting noise."""
ts = x.new_ones([x.shape[0]])
# Create the noise schedule
t = torch.linspace(1, 0, steps + 1)[:-1]
alphas, sigmas = get_alphas_sigmas(t)
# The sampling loop
for i in trange(steps):
# Get the model output (v, the predicted velocity)
##########################################################################
# TODO: Perform classifier-free guidance: #
# 1.) Generate inputs for both conditional images and unconditional #
# images given their class. #
# Hint: To generate unconditional input, copy the input images and time #
# stamps and stack them with the original input images and time stamps. #
# The only thing you need to change is the create the unconditional #
# class "-1" and stack it with the input conditional class. Thus You #
# will have a tensor of twice of the batch size of the original input. #
# 2.) Pass your stacked input to the model to get both conditional and #
# unconditional vecocity. #
# 3.) Compute v = v_uncond + guidance_scale * (v_cond - v_uncond) #
##########################################################################
# Replace "pass" statement with your code
x_dupl = x.clone()
x_stacked = torch.cat([x, x_dupl], dim = 0)
ts_dupl = ts.clone()
ts_stacked = torch.cat([ts, ts_dupl], dim = 0)
ts_stacked = ts_stacked * sigmas[i]
classes_unconditional = -1 * torch.ones_like(classes)
classes_stacked = torch.cat([classes, classes_unconditional], dim = 0)
res = model(x_stacked, ts_stacked, classes_stacked)
v_cond = res[:100, :, :]
v_uncond = res[100:, :, :]
v = v_uncond + guidance_scale * (v_cond - v_uncond)
##########################################################################
# END OF YOUR CODE #
##########################################################################
# Predict the noise and the denoised image
pred = x * alphas[i] - v * sigmas[i]
eps = x * sigmas[i] + v * alphas[i]
# If we are not on the last timestep, compute the noisy image for the
# next timestep.
if i < steps - 1:
# If eta > 0, adjust the scaling factor for the predicted noise
# downward according to the amount of additional noise to add
ddim_sigma = eta * (sigmas[i + 1]**2 / sigmas[i]**2).sqrt() * \
(1 - alphas[i]**2 / alphas[i + 1]**2).sqrt()
adjusted_sigma = (sigmas[i + 1]**2 - ddim_sigma**2).sqrt()
# Recombine the predicted noise and predicted denoised image in the
# correct proportions for the next step
x = pred * alphas[i + 1] + eps * adjusted_sigma
# Add the correct amount of fresh noise
if eta:
x += torch.randn_like(x) * ddim_sigma
# If we are on the last timestep, output the denoised image
return pred
# Visualize the noise schedule
%config InlineBackend.figure_format = 'retina'
plt.rcParams['figure.dpi'] = 100
t_vis = torch.linspace(0, 1, 1000)
alphas_vis, sigmas_vis = get_alphas_sigmas(t_vis)
print('The noise schedule:')
plt.plot(t_vis, alphas_vis, label='alpha (signal level)')
plt.plot(t_vis, sigmas_vis, label='sigma (noise level)')
plt.legend()
plt.xlabel('timestep')
plt.grid()
plt.show()
The noise schedule:
# Prepare the dataset
batch_size = 100
tf = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize([0.5], [0.5]),
])
train_set = datasets.CIFAR10('data', train=True, download=True, transform=tf)
train_dl = data.DataLoader(train_set, batch_size, shuffle=True,
num_workers=4, persistent_workers=True, pin_memory=True)
val_set = datasets.CIFAR10('data', train=False, download=True, transform=tf)
val_dl = data.DataLoader(val_set, batch_size,
num_workers=4, persistent_workers=True, pin_memory=True)
Files already downloaded and verified
/usr/local/lib/python3.8/dist-packages/torch/utils/data/dataloader.py:554: UserWarning: This DataLoader will create 4 worker processes in total. Our suggested max number of worker in current system is 2, which is smaller than what this DataLoader is going to create. Please be aware that excessive worker creation might get DataLoader running slow or even freeze, lower the worker number to avoid potential slowness/freeze if necessary.
warnings.warn(_create_warning_msg(
Files already downloaded and verified
# Create the model and optimizer
seed = 0
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print('Using device:', device)
torch.manual_seed(0)
model = Diffusion().to(device)
model_ema = deepcopy(model)
print('Model parameters:', sum(p.numel() for p in model.parameters()))
opt = optim.Adam(model.parameters(), lr=2e-4)
scaler = torch.cuda.amp.GradScaler()
epoch = 0
# Use a low discrepancy quasi-random sequence to sample uniformly distributed
# timesteps. This considerably reduces the between-batch variance of the loss.
rng = torch.quasirandom.SobolEngine(1, scramble=True)
Using device: cuda
Model parameters: 27487287
As a sanity check, the total number of parameters in your model should match the following.
Model parameters: 27487287
1.(c) Training
# Actually train the model
ema_decay = 0.999
# The number of timesteps to use when sampling
steps = 500
# The amount of noise to add each timestep when sampling
# 0 = no noise (DDIM)
# 1 = full noise (DDPM)
eta = 1.
# Classifier-free guidance scale (0 is unconditional, 1 is conditional)
guidance_scale = 2.
def eval_loss(model, rng, reals, classes):
# Draw uniformly distributed continuous timesteps
t = rng.draw(reals.shape[0])[:, 0].to(device)
# Calculate the noise schedule parameters for those timesteps
alphas, sigmas = get_alphas_sigmas(t)
# Combine the ground truth images and the noise
alphas = alphas[:, None, None, None]
sigmas = sigmas[:, None, None, None]
noise = torch.randn_like(reals)
noised_reals = reals * alphas + noise * sigmas
targets = noise * alphas - reals * sigmas
# Drop out the class on 20% of the examples
to_drop = torch.rand(classes.shape, device=classes.device).le(0.2)
classes_drop = torch.where(to_drop, -torch.ones_like(classes), classes)
# Compute the model output and the loss.
v = model(noised_reals, t, classes_drop)
return F.mse_loss(v, targets)
def train():
for i, (reals, classes) in enumerate(tqdm(train_dl)):
opt.zero_grad()
reals = reals.to(device)
classes = classes.to(device)
# Evaluate the loss
loss = eval_loss(model, rng, reals, classes)
# Do the optimizer step and EMA update
scaler.scale(loss).backward()
scaler.step(opt)
ema_update(model, model_ema, 0.95 if epoch < 5 else ema_decay)
scaler.update()
if i % 50 == 0:
tqdm.write(f'Epoch: {epoch}, iteration: {i}, loss: {loss.item():g}')
@torch.no_grad()
@torch.random.fork_rng()
@eval_mode(model_ema)
def val():
tqdm.write('\nValidating...')
torch.manual_seed(seed)
rng = torch.quasirandom.SobolEngine(1, scramble=True)
total_loss = 0
count = 0
for i, (reals, classes) in enumerate(tqdm(val_dl)):
reals = reals.to(device)
classes = classes.to(device)
loss = eval_loss(model_ema, rng, reals, classes)
total_loss += loss.item() * len(reals)
count += len(reals)
loss = total_loss / count
tqdm.write(f'Validation: Epoch: {epoch}, loss: {loss:g}')
@torch.no_grad()
@torch.random.fork_rng()
@eval_mode(model_ema)
def demo():
tqdm.write('\nSampling...')
torch.manual_seed(seed)
noise = torch.randn([100, 3, 32, 32], device=device)
fakes_classes = torch.arange(10, device=device).repeat_interleave(10, 0)
fakes = sample(model_ema, noise, steps, eta, fakes_classes, guidance_scale)
grid = utils.make_grid(fakes, 10).cpu()
filename = f'demo_{epoch:05}.png'
TF.to_pil_image(grid.add(1).div(2).clamp(0, 1)).save(filename)
display.display(display.Image(filename))
tqdm.write('')
# Each epoch might take up to 2.5 minutes
print("Initial noise")
val()
demo()
while epoch <= 20:
print('Epoch', epoch)
train()
if epoch % 5 == 0:
val()
demo()
epoch += 1
Initial noise
Validating...
0%| | 0/100 [00:00<?, ?it/s]
Validation: Epoch: 0, loss: 0.658896
Sampling...
0%| | 0/500 [00:00<?, ?it/s]

Epoch 0
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 0, iteration: 0, loss: 0.653755
Epoch: 0, iteration: 50, loss: 0.338001
Epoch: 0, iteration: 100, loss: 0.21632
Epoch: 0, iteration: 150, loss: 0.198722
Epoch: 0, iteration: 200, loss: 0.19362
Epoch: 0, iteration: 250, loss: 0.183347
Epoch: 0, iteration: 300, loss: 0.181369
Epoch: 0, iteration: 350, loss: 0.188113
Epoch: 0, iteration: 400, loss: 0.177421
Epoch: 0, iteration: 450, loss: 0.178177
Validating...
0%| | 0/100 [00:00<?, ?it/s]
Validation: Epoch: 0, loss: 0.156966
Sampling...
0%| | 0/500 [00:00<?, ?it/s]

Epoch 1
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 1, iteration: 0, loss: 0.162407
Epoch: 1, iteration: 50, loss: 0.17322
Epoch: 1, iteration: 100, loss: 0.16159
Epoch: 1, iteration: 150, loss: 0.166741
Epoch: 1, iteration: 200, loss: 0.169998
Epoch: 1, iteration: 250, loss: 0.157178
Epoch: 1, iteration: 300, loss: 0.15836
Epoch: 1, iteration: 350, loss: 0.14725
Epoch: 1, iteration: 400, loss: 0.155168
Epoch: 1, iteration: 450, loss: 0.155566
Epoch 2
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 2, iteration: 0, loss: 0.140601
Epoch: 2, iteration: 50, loss: 0.155231
Epoch: 2, iteration: 100, loss: 0.157367
Epoch: 2, iteration: 150, loss: 0.151691
Epoch: 2, iteration: 200, loss: 0.144565
Epoch: 2, iteration: 250, loss: 0.149661
Epoch: 2, iteration: 300, loss: 0.136923
Epoch: 2, iteration: 350, loss: 0.15234
Epoch: 2, iteration: 400, loss: 0.145771
Epoch: 2, iteration: 450, loss: 0.145041
Epoch 3
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 3, iteration: 0, loss: 0.143917
Epoch: 3, iteration: 50, loss: 0.1509
Epoch: 3, iteration: 100, loss: 0.136954
Epoch: 3, iteration: 150, loss: 0.135847
Epoch: 3, iteration: 200, loss: 0.131022
Epoch: 3, iteration: 250, loss: 0.141681
Epoch: 3, iteration: 300, loss: 0.135785
Epoch: 3, iteration: 350, loss: 0.154194
Epoch: 3, iteration: 400, loss: 0.141047
Epoch: 3, iteration: 450, loss: 0.148207
Epoch 4
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 4, iteration: 0, loss: 0.138591
Epoch: 4, iteration: 50, loss: 0.133283
Epoch: 4, iteration: 100, loss: 0.141574
Epoch: 4, iteration: 150, loss: 0.144843
Epoch: 4, iteration: 200, loss: 0.137238
Epoch: 4, iteration: 250, loss: 0.141183
Epoch: 4, iteration: 300, loss: 0.155489
Epoch: 4, iteration: 350, loss: 0.140727
Epoch: 4, iteration: 400, loss: 0.138877
Epoch: 4, iteration: 450, loss: 0.126518
Epoch 5
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 5, iteration: 0, loss: 0.131273
Epoch: 5, iteration: 50, loss: 0.132139
Epoch: 5, iteration: 100, loss: 0.128993
Epoch: 5, iteration: 150, loss: 0.148662
Epoch: 5, iteration: 200, loss: 0.144224
Epoch: 5, iteration: 250, loss: 0.136586
Epoch: 5, iteration: 300, loss: 0.124944
Epoch: 5, iteration: 350, loss: 0.13695
Epoch: 5, iteration: 400, loss: 0.134327
Epoch: 5, iteration: 450, loss: 0.144528
Validating...
0%| | 0/100 [00:00<?, ?it/s]
Validation: Epoch: 5, loss: 0.127014
Sampling...
0%| | 0/500 [00:00<?, ?it/s]

Epoch 6
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 6, iteration: 0, loss: 0.134014
Epoch: 6, iteration: 50, loss: 0.135877
Epoch: 6, iteration: 100, loss: 0.131052
Epoch: 6, iteration: 150, loss: 0.141449
Epoch: 6, iteration: 200, loss: 0.11968
Epoch: 6, iteration: 250, loss: 0.124398
Epoch: 6, iteration: 300, loss: 0.119443
Epoch: 6, iteration: 350, loss: 0.130245
Epoch: 6, iteration: 400, loss: 0.1426
Epoch: 6, iteration: 450, loss: 0.129
Epoch 7
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 7, iteration: 0, loss: 0.143265
Epoch: 7, iteration: 50, loss: 0.146954
Epoch: 7, iteration: 100, loss: 0.135964
Epoch: 7, iteration: 150, loss: 0.127498
Epoch: 7, iteration: 200, loss: 0.132977
Epoch: 7, iteration: 250, loss: 0.127253
Epoch: 7, iteration: 300, loss: 0.132274
Epoch: 7, iteration: 350, loss: 0.131093
Epoch: 7, iteration: 400, loss: 0.135549
Epoch: 7, iteration: 450, loss: 0.142583
Epoch 8
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 8, iteration: 0, loss: 0.127067
Epoch: 8, iteration: 50, loss: 0.130348
Epoch: 8, iteration: 100, loss: 0.121566
Epoch: 8, iteration: 150, loss: 0.128043
Epoch: 8, iteration: 200, loss: 0.122754
Epoch: 8, iteration: 250, loss: 0.132863
Epoch: 8, iteration: 300, loss: 0.1272
Epoch: 8, iteration: 350, loss: 0.143117
Epoch: 8, iteration: 400, loss: 0.129728
Epoch: 8, iteration: 450, loss: 0.130927
Epoch 9
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 9, iteration: 0, loss: 0.121929
Epoch: 9, iteration: 50, loss: 0.134126
Epoch: 9, iteration: 100, loss: 0.127221
Epoch: 9, iteration: 150, loss: 0.143794
Epoch: 9, iteration: 200, loss: 0.127967
Epoch: 9, iteration: 250, loss: 0.141
Epoch: 9, iteration: 300, loss: 0.130928
Epoch: 9, iteration: 350, loss: 0.114041
Epoch: 9, iteration: 400, loss: 0.121675
Epoch: 9, iteration: 450, loss: 0.134999
Epoch 10
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 10, iteration: 0, loss: 0.120093
Epoch: 10, iteration: 50, loss: 0.126596
Epoch: 10, iteration: 100, loss: 0.140558
Epoch: 10, iteration: 150, loss: 0.127961
Epoch: 10, iteration: 200, loss: 0.138925
Epoch: 10, iteration: 250, loss: 0.128185
Epoch: 10, iteration: 300, loss: 0.130993
Epoch: 10, iteration: 350, loss: 0.13117
Epoch: 10, iteration: 400, loss: 0.127555
Epoch: 10, iteration: 450, loss: 0.131825
Validating...
0%| | 0/100 [00:00<?, ?it/s]
Validation: Epoch: 10, loss: 0.122518
Sampling...
0%| | 0/500 [00:00<?, ?it/s]

Epoch 11
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 11, iteration: 0, loss: 0.131141
Epoch: 11, iteration: 50, loss: 0.119489
Epoch: 11, iteration: 100, loss: 0.133515
Epoch: 11, iteration: 150, loss: 0.131604
Epoch: 11, iteration: 200, loss: 0.121556
Epoch: 11, iteration: 250, loss: 0.127839
Epoch: 11, iteration: 300, loss: 0.116606
Epoch: 11, iteration: 350, loss: 0.139214
Epoch: 11, iteration: 400, loss: 0.129358
Epoch: 11, iteration: 450, loss: 0.134403
Epoch 12
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 12, iteration: 0, loss: 0.124086
Epoch: 12, iteration: 50, loss: 0.136179
Epoch: 12, iteration: 100, loss: 0.118663
Epoch: 12, iteration: 150, loss: 0.129204
Epoch: 12, iteration: 200, loss: 0.134248
Epoch: 12, iteration: 250, loss: 0.129005
Epoch: 12, iteration: 300, loss: 0.130204
Epoch: 12, iteration: 350, loss: 0.136777
Epoch: 12, iteration: 400, loss: 0.124229
Epoch: 12, iteration: 450, loss: 0.124824
Epoch 13
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 13, iteration: 0, loss: 0.124579
Epoch: 13, iteration: 50, loss: 0.126965
Epoch: 13, iteration: 100, loss: 0.131171
Epoch: 13, iteration: 150, loss: 0.121483
Epoch: 13, iteration: 200, loss: 0.12589
Epoch: 13, iteration: 250, loss: 0.135764
Epoch: 13, iteration: 300, loss: 0.133478
Epoch: 13, iteration: 350, loss: 0.122517
Epoch: 13, iteration: 400, loss: 0.12022
Epoch: 13, iteration: 450, loss: 0.126342
Epoch 14
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 14, iteration: 0, loss: 0.131133
Epoch: 14, iteration: 50, loss: 0.128552
Epoch: 14, iteration: 100, loss: 0.13153
Epoch: 14, iteration: 150, loss: 0.131903
Epoch: 14, iteration: 200, loss: 0.12955
Epoch: 14, iteration: 250, loss: 0.125184
Epoch: 14, iteration: 300, loss: 0.121807
Epoch: 14, iteration: 350, loss: 0.122976
Epoch: 14, iteration: 400, loss: 0.133133
Epoch: 14, iteration: 450, loss: 0.1367
Epoch 15
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 15, iteration: 0, loss: 0.128771
Epoch: 15, iteration: 50, loss: 0.126213
Epoch: 15, iteration: 100, loss: 0.121458
Epoch: 15, iteration: 150, loss: 0.118837
Epoch: 15, iteration: 200, loss: 0.126703
Epoch: 15, iteration: 250, loss: 0.14023
Epoch: 15, iteration: 300, loss: 0.12236
Epoch: 15, iteration: 350, loss: 0.130496
Epoch: 15, iteration: 400, loss: 0.127596
Epoch: 15, iteration: 450, loss: 0.134363
Validating...
0%| | 0/100 [00:00<?, ?it/s]
Validation: Epoch: 15, loss: 0.119766
Sampling...
0%| | 0/500 [00:00<?, ?it/s]

Epoch 16
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 16, iteration: 0, loss: 0.125691
Epoch: 16, iteration: 50, loss: 0.118597
Epoch: 16, iteration: 100, loss: 0.126822
Epoch: 16, iteration: 150, loss: 0.131161
Epoch: 16, iteration: 200, loss: 0.12752
Epoch: 16, iteration: 250, loss: 0.125761
Epoch: 16, iteration: 300, loss: 0.133977
Epoch: 16, iteration: 350, loss: 0.12774
Epoch: 16, iteration: 400, loss: 0.123883
Epoch: 16, iteration: 450, loss: 0.128178
Epoch 17
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 17, iteration: 0, loss: 0.133109
Epoch: 17, iteration: 50, loss: 0.122719
Epoch: 17, iteration: 100, loss: 0.128501
Epoch: 17, iteration: 150, loss: 0.126248
Epoch: 17, iteration: 200, loss: 0.138365
Epoch: 17, iteration: 250, loss: 0.125818
Epoch: 17, iteration: 300, loss: 0.123439
Epoch: 17, iteration: 350, loss: 0.115521
Epoch: 17, iteration: 400, loss: 0.126633
Epoch: 17, iteration: 450, loss: 0.132971
Epoch 18
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 18, iteration: 0, loss: 0.117829
Epoch: 18, iteration: 50, loss: 0.130679
Epoch: 18, iteration: 100, loss: 0.130787
Epoch: 18, iteration: 150, loss: 0.141084
Epoch: 18, iteration: 200, loss: 0.115277
Epoch: 18, iteration: 250, loss: 0.117496
Epoch: 18, iteration: 300, loss: 0.118217
Epoch: 18, iteration: 350, loss: 0.126384
Epoch: 18, iteration: 400, loss: 0.127696
Epoch: 18, iteration: 450, loss: 0.138881
Epoch 19
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 19, iteration: 0, loss: 0.134403
Epoch: 19, iteration: 50, loss: 0.125974
Epoch: 19, iteration: 100, loss: 0.115442
Epoch: 19, iteration: 150, loss: 0.112067
Epoch: 19, iteration: 200, loss: 0.130088
Epoch: 19, iteration: 250, loss: 0.122191
Epoch: 19, iteration: 300, loss: 0.130753
Epoch: 19, iteration: 350, loss: 0.133672
Epoch: 19, iteration: 400, loss: 0.126002
Epoch: 19, iteration: 450, loss: 0.131824
Epoch 20
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 20, iteration: 0, loss: 0.126931
Epoch: 20, iteration: 50, loss: 0.117533
Epoch: 20, iteration: 100, loss: 0.125484
Epoch: 20, iteration: 150, loss: 0.124927
Epoch: 20, iteration: 200, loss: 0.130618
Epoch: 20, iteration: 250, loss: 0.120571
Epoch: 20, iteration: 300, loss: 0.134657
Epoch: 20, iteration: 350, loss: 0.118322
Epoch: 20, iteration: 400, loss: 0.122906
Epoch: 20, iteration: 450, loss: 0.122052
Validating...
0%| | 0/100 [00:00<?, ?it/s]
Validation: Epoch: 20, loss: 0.118255
Sampling...
0%| | 0/500 [00:00<?, ?it/s]

Problem2: Epipolar Geometry
In this problem, you will plot epipolar lines. Given an input pixel in a reference view, we will plot the line containing all of its possible correspondences in a second view.
The reference view will be located at the origin, with an identity rotation matrix:
\[P_{1} = K[I|0], \\\]while the second view’s projection matrix is given by:
\[P_{2} = K[R|t].\]Both cameras have the same intrinsics matrix K.
Download the temple stereo images from the Middlebury stereo dataset.
!wget https://vision.middlebury.edu/mview/data/data/templeSparseRing.zip
!unzip templeSparseRing.zip
--2022-12-10 06:46:50-- https://vision.middlebury.edu/mview/data/data/templeSparseRing.zip
Resolving vision.middlebury.edu (vision.middlebury.edu)... 140.233.20.14
Connecting to vision.middlebury.edu (vision.middlebury.edu)|140.233.20.14|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 4004383 (3.8M) [application/zip]
Saving to: ‘templeSparseRing.zip’
templeSparseRing.zi 100%[===================>] 3.82M 1.97MB/s in 1.9s
2022-12-10 06:46:54 (1.97 MB/s) - ‘templeSparseRing.zip’ saved [4004383/4004383]
Archive: templeSparseRing.zip
creating: templeSparseRing/
inflating: templeSparseRing/templeSR_ang.txt
inflating: templeSparseRing/templeSR0001.png
inflating: templeSparseRing/templeSR0002.png
inflating: templeSparseRing/templeSR0003.png
inflating: templeSparseRing/templeSR0004.png
inflating: templeSparseRing/templeSR0005.png
inflating: templeSparseRing/templeSR0006.png
inflating: templeSparseRing/templeSR0007.png
inflating: templeSparseRing/templeSR0008.png
inflating: templeSparseRing/templeSR0009.png
inflating: templeSparseRing/templeSR0010.png
inflating: templeSparseRing/templeSR0011.png
inflating: templeSparseRing/templeSR0012.png
inflating: templeSparseRing/templeSR0013.png
inflating: templeSparseRing/templeSR0014.png
inflating: templeSparseRing/templeSR0015.png
inflating: templeSparseRing/templeSR0016.png
inflating: templeSparseRing/templeSR_par.txt
inflating: templeSparseRing/README.txt
def process_parameters():
"""
Reads the parameters for the Middlebury dataset
:return: an intrinsics matrix containing the camera parameters and
a list of extrinsics matrices representing mapping from the world to camera coordinates
"""
intrinsics = []
extrinsics = []
with open(os.path.join("templeSparseRing", "templeSR_par.txt"), 'r') as f:
_ = f.readline()
for line in f:
raw_data = line.split()
# Read camera parameters K (intrinsics matrix)
camera_params = np.array(raw_data[1:10]).reshape((3, 3)).astype(float)
intrinsics.append(camera_params)
# Read homogeneous transformation (extrinsics matrix)
rotation = np.array(raw_data[10:19]).reshape((3, 3)).astype(float)
translation = np.array(raw_data[19:]).reshape((3, 1)).astype(float)
extrinsics.append(np.hstack([rotation, translation]))
return intrinsics[0], extrinsics
We will select the first image as the reference frame and transform all the extrinsics matrices.
def set_reference(extrinsics):
"""
Set the first image as reference frame such that its transformation
becomes the identity, apply the inverse of the extrinsics matrix of
the reference frame to all other extrinsics matrices
:param extrinsics: list of original extrinsics matrices
:return: list of transformed extrinsics matrices
"""
shifted_extrinsics = []
stacked = np.vstack([extrinsics[0], [0, 0, 0, 1]])
inv_ref = np.linalg.inv(stacked)
for ex in extrinsics:
stacked = np.vstack([ex, [0, 0, 0, 1]])
transformed = np.matmul(stacked, inv_ref)
transformed /= transformed[-1, -1]
shifted_extrinsics.append(transformed[:3, :])
return shifted_extrinsics
2.(a) Back-projection
Fill in the coordinate transform function. First, obtain the ray $v = K^{-1}p$ that connects the reference camera’s center of projection to pixel p on the image plane (using homogeneous coordinates for p). We will walk along the ray at various distances $d_1, d_2, …, d_N$ . For each one, create a 3D point $X_{i} = d_{i}v$. Project it into the second view. The provided code will then draw a dot at this position. After processing all N depth values, you should see a line. The correspondence to $p$ should lie somewhere on this line.
def coordinate_transform(intrinsics, extrinsics, pixel, d, i):
"""
Transform image coordiantes from the reference frame to the second image given a depth d
:param intrinsics: the matrix K storing the camera parameters
:param extrinsics: list of 3 x 4 extrinsics matricies [R | t]
:param pixel: tuple of two ints representing x and y coordinates on the reference image
:param d: a float representing a distance
:param i: int at the end of the image name (4 represents templeSR0004.png)
:return: pixel_coord, a tuple of ints representing the x, y coordinates on the second image
"""
extrinsics_img2 = extrinsics[i - 1]
##########################################################################
# TODO: Implement the coordinate transformation #
##########################################################################
# Replace "pass" statement with your code
# Back-project pixel x in reference frame to world coordinates X
# X = K^-1 @ x * d
# Forward project point X to the second image's pixel coordinates x
# pixel_coord = K @ extrinsics_img2 @ X
X = np.linalg.inv(intrinsics) @ [pixel[0], pixel[1], 1] * d
pixel_coord = intrinsics @ extrinsics_img2 @ [X[0], X[1], X[2], 1]
pixel_coord = np.array([pixel_coord[0] / pixel_coord[2], pixel_coord[1] / pixel_coord[2]])
##########################################################################
# END OF YOUR CODE #
##########################################################################
return pixel_coord.astype(int)
2.(b) Compute fundamental matrix
Fill in the compute fundamental matrix function. We will estimate the fundamental matrix $F \in \mathbb{R}^{3 x 3}$ from camera pose. Note that it is also possible to directly estimate $F$ from correspondences, without the full camera pose. First compute the epipole:
\[e = KR^{T}t\]We will then compute $F$ between another image frame with respect to the reference frame.
\[F = K^{-T}RK^{T}[e]_{x}\]where $[e]_{x}$ is the cross product of the epipole.
def compute_fundamental_matrix(intrinsics, extrinsics, i):
"""
Compute the fundamental matrix between the i-th image frame and the
reference image frame
:param intrinsics: the intrinsics camera matrix
:param extrinsics: list of original extrinsics matrices
:param i: int at the end of the image name (2 represents templeSR0002.png)
:return: list of transformed extrinsics matrices
"""
rot = extrinsics[i - 1][:3, :3]
trans = extrinsics[i - 1][:3, 3]
# Compute the epipole and fundamental matrix
# e = K R^T t
epipole = intrinsics @ rot.T @ trans
epipole_cross = np.array([[0, -epipole[2], epipole[1]], [epipole[2], 0, -epipole[0]], [-epipole[1], epipole[0], 0]])
# F = K'^(-T)RK^T[e]_x
fundamental = np.linalg.inv(intrinsics).T @ rot @ intrinsics.T @ epipole_cross
fundamental /= fundamental[-1, -1]
return fundamental
2.(c) Visualize epipolar line
Fill in the visualize epipolar line function. For any pixel $p$ in the reference frame, we can compute the line $u = F p$. The pixel in the other image that corresponds to $p$ falls along $u$. The vector $u = [a, b, c]^{T}$ represents a line in the form $ax + by + c = 0$.
def visualize_epipolar_line(pixel, intrinsics, extrinsics, fundamental, i):
"""
Visualizes the pixel in the reference frame, and its corresponding
epipolar line in the i-th image frame
:param pixel: a tuple of (x, y) coordinates in the reference image
:param fundamental: fundamental matrix
:param i: int at the end of the image name (4 represents templeSR0004.png)
"""
img1 = imread(os.path.join("templeSparseRing", "templeSR0001.png"))
img2 = imread(sorted(glob(os.path.join("templeSparseRing", "*.png")))[i - 1])
# Plot reference image with a chosen pixel
_, ax = plt.subplots(1, 3, figsize=(img1.shape[1] * 3 / 80, img1.shape[0] / 80))
ax[0].imshow(img1)
ax[0].add_patch(patches.Rectangle(pixel, 5, 5))
ax[0].title.set_text('Reference Frame')
# Compute epipolar_line from fundamental matrix and the pixel coordinates
# Hartley Zisserman page 246: "I' = Fx is the epipolar line corresponding to x"
# Epipolar line l' in image 2's coordinates
epipolar_line = fundamental @ np.array([pixel[0], pixel[1], 1]).T
# Plot epipolar line from fundamental matrix in second image
x = np.arange(img2.shape[1])
y = np.array((-epipolar_line[0] * x - epipolar_line[2]) / epipolar_line[1])
indices = np.where(np.logical_and(y >= 0, y <= img2.shape[0]))
ax[1].imshow(img2)
ax[1].plot(x[indices], y[indices])
ax[1].title.set_text('Epipolar Line from Fundamental Matrix in templeSR000' + str(i))
# Epipolar line from backprojected ray of different depths
ax[2].imshow(img2)
ax[2].title.set_text('Epipolar Line from Backprojected Ray in templeSR000' + str(i))
for d in np.arange(0.4, 0.8, 0.005):
pixel_coord = coordinate_transform(intrinsics, extrinsics, pixel, d, i)
if pixel_coord[0] >= 0 and pixel_coord[1] >= 0 and pixel_coord[0] + 3 < \
img1.shape[1] and pixel_coord[1] + 3:
ax[2].add_patch(patches.Rectangle((pixel_coord[0], pixel_coord[1]), 3, 3))
plt.show()
# TODO: Feel free to try different images and pixel coordinates
# image_frame is the image number (i.e. 4 is templeSR0004.png)
image_frame = 4
# pixel location (x, y) in the reference frame
pixel = (500, 200)
intrinsics, extrinsics = process_parameters()
shifted_extrinsics = set_reference(extrinsics)
fundamental = compute_fundamental_matrix(intrinsics, shifted_extrinsics, i=image_frame)
visualize_epipolar_line(pixel, intrinsics, shifted_extrinsics, fundamental, i=image_frame)

